Verwenden der Rechnerfunktion
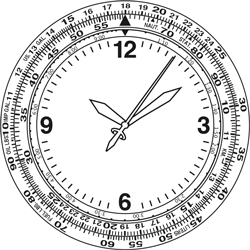
Hinweis: Bei bestimmten Modellen sind die innere und die äußere Skala gegeneinander vertauscht. Bitte berücksichtigen Sie diese Tatsache sorgfältig, wenn Sie die nachstehenden Anweisungen befolgen.
Einfache Berechnungen
[Multiplizieren]
![[Multiplizieren]](/cms/global/support/exterior/images/ext_calc_multiple.png)
Aufgabe :
20 × 15
Lösung :
Bringen Sie die Teilung „20“ der äußeren Skala mit der Teilung „10“ der inneren Skala zur Deckung.
Jetzt weist die Teilung „30“ der äußeren Skala auf die Teilung „15“ der inneren Skala, und durch Hinzufügen einer Null wird „300“ als Ergebnis erhalten.
[Dividieren]
![[How to do division]](/cms/global/support/exterior/images/ext_calc_div.png)
Aufgabe :
250 ÷ 20
Lösung :
Bringen Sie die Teilung „25“ der äußeren Skala mit der Teilung „20“ der inneren Skala zur Deckung.
Jetzt weist die Teilung „12,5“ der äußeren Skala auf die Teilung „10“ der inneren Skala, und „12,5“ wird als Ergebnis erhalten.
[Verhältnisrechnung]
![[Verhältnisrechnung]](/cms/global/support/exterior/images/ext_calc_ratio.png)
Aufgabe :
30/20 = 60/A
Lösung :
Bringen Sie die Teilung „30“ der äußeren Skala mit der Teilung „20“ der inneren Skala zur Deckung.
Jetzt weist die Teilung „40“ der inneren Skala auf die Teilung „60“ der äußeren Skala, und an allen Positionen oberhalb der Skala stehen die Teilungen der inneren und äußeren Skala jeweils im gleichen Verhältnis zueinander wie 30 und 20. Auf diese Weise können Sie das Ergebnis anderer Verhältnisrechnungen bequem ablesen.
[Umwandeln eines Volumens zwischen verschiedenen Messeinheiten]
![[Umwandeln eines Volumens zwischen verschiedenen Messeinheiten]](/cms/global/support/exterior/images/ext_calc_fuelpound.png)
Sie können ein Kraftstoffvolumen zwischen Pounds (lbs), U.S. Gallons (U.S.GAL.), Imperial Gallons (IMP.GAL) oder Litern umrechnen.
Aufgabe :
Wie viele U.S. Gallons, Imperial Gallons oder Liter entsprechen 13,1 lbs Kraftstoff ?
(1 FUEL LBS entspricht 0,167 U.S.GAL. / 0,139 IMP.GAL. /0,632 Liter.)
Lösung :
Bringen Sie die Markierung„▼“ von FUEL LBS. an der äußeren Skala mit der Teilung „13,1“, der umzuwandelnden Menge, der inneren Skala zur Deckung.
Lesen Sie die der Markierung „▼“ von U.S.GAL. an der äußeren Skala entsprechende Teilung ab.
Nach Hinzufügen einer Einheit wird „2,18 U.S.GAL.“ als Ergebnis erhalten.
Auf gleiche Weise können Sie die jeweils der Markierung „▼“ von IMP.GAL. und LITERS entsprechende Teilung ablesen, um „1,82 IMP.GAL.“ bzw. „8,28 Liter.“ als Ergebnis zu erhalten.
[Umwandeln eines Gewichts zwischen verschiedenen Messeinheiten]
![[Umwandeln eines Gewichts zwischen verschiedenen Messeinheiten]](/cms/global/support/exterior/images/ext_calc_oilpound.png)
Sie können eine in Pounds angegebene Menge Öl (OIL.LBS.) in U.S. Gallons, Imperial Gallons oder Litern umrechnen.
Aufgabe :
Wie viele U.S. Gallons, Imperial Gallons oder Liter entsprechen 16,4 lbs Öl ?
(1 OIL.LBS. entspricht 0,133 U.S.GAL., 0,111 IMP.GAL. bzw. 0.503 Liter.)
Lösung :
Bringen Sie die Markierung„▼“ von OIL.LBS. an der äußeren Skala mit der Teilung „16,4“, der umzuwandelnden Menge, der inneren Skala zur Deckung.
Lesen Sie die der Markierung „▼“ von U.S.GAL. an der äußeren Skala entsprechende Teilung ab. Nach Hinzufügen einer Einheit wird „2,18 U.S.GAL“ als Ergebnis erhalten.
Auf gleiche Weise können Sie die jeweils der Markierung „▼“ von IMP.GAL. und LITERS entsprechende Teilung ablesen, um „1,82 IMP.GAL.“ bzw. „8,25 Liter“ als Ergebnis zu erhalten.
[Umwandeln einer Entfernung zwischen verschiedenen Messeinheiten]
![[Umwandeln einer Entfernung zwischen verschiedenen Messeinheiten]](/cms/global/support/exterior/images/ext_calc_distance.png)
Sie können Entfernungen zwischen Kilometern, Seemeilen und englischen Meilen umrechnen.
Aufgabe :
Wie viele Kilometer und Seemeilen entsprechen jeweils 1 englische Meile ?
Lösung :
Bringen Sie die Markierung „▼“ der Teilung „10“ an der äußeren Skala mit der Markierung „▲“ von STAT an der inneren Skala zur Deckung. Ergebnis: Die Teilung „16“ der Skala entspricht der Markierung „▲“ von KM an der inneren Skala.
Nachdem Sie den Dezimalpunkt um eine Stelle verschoben haben, wird „1,6 km“ als Ergebnis erhalten.
Ebenso können Sie die Antwort 86,6 NAUT (0,866 Seemeilen) entsprechend dem „▲“ von NAUT erhalten.
[Umwandeln einer Kraftstoffmenge zwischen verschiedenen Messeinheiten]
![[Umwandeln einer Kraftstoffmenge zwischen verschiedenen Messeinheiten]](/cms/global/support/exterior/images/ext_calc_vol.png)
Sie können zwischen Litern, U.S. Gallons und Imperial Gallons umrechnen.
Aufgabe :
Wie viele Liter entsprechen 16,8 U.S. Gallons ?
Lösung :
Bringen Sie die Markierung „▼“ von U.S. GAL an der äußeren Skala mit der Teilung „16,8“, der umzuwandelnden Menge, der inneren Skala zur Deckung.
Ergebnis: Nach der Umwandlung wird der der Markierung „▼“ von Liter an der äußeren Skala entsprechende Wert (ca. 63,5) erhalten (1 U.S. GAL = 3,78541 Liter).
Verwenden der Motorsport-Funktion
[Berechnung der Zeitdauer, die zum Zurücklegen einer bestimmten Strecke erforderlich ist]
![[Berechnung der Zeitdauer, die zum Zurücklegen einer bestimmten Strecke erforderlich ist]](/cms/global/support/exterior/images/ext_motor_time.png)
Aufgabe :
Wie lange braucht ein Fahrzeug, das sich mit einer Geschwindigkeit von 80 km/h bewegt, um 400 km zurückzulegen ?
Lösung :
Bringen Sie die Teilung „80“ an der äußeren Skala mit der Markierung „▲“ von SPEED INDEX an der inneren Skala zur Deckung. Ergebnis: 5 Stunden (5,00) an der inneren Skala entspricht der Teilung„40“ an der äußeren Skala.
[Berechnung einer Durchschnittsgeschwindigkeit]
![[Berechnung einer Durchschnittsgeschwindigkeit]](/cms/global/support/exterior/images/ext_motor_speed.png)
Aufgabe :
Wie hoch ist die Durchschnittsgeschwindigkeit eines Fahrzeugs, das eine Strecke von 180 km in einer Zeit von 2 Std. 30 Minuten zurückgelegt hat?
Lösung :
Bringen Sie die Teilung „18“ an der äußeren Skala mit der Teilung„2:30“ an der inneren Skala zur Deckung.
Ergebnis: Wenn die Markierung „▲“ von SPEED INDEX an der inneren Skala mit der entsprechenden Teilung an der äußeren Skala zur Deckung gebracht wird, ergibt sich 72 km/h als Durchschnittsgeschwindigkeit.
[Berechnung einer Fahrstrecke]
![[Berechnung einer Fahrstrecke]](/cms/global/support/exterior/images/ext_motor_distance.png)
Aufgabe :
Welche Entfernung legt ein Fahrzeug, das sich mit einer Durchschnittsgeschwindigkeit von 60 km/h bewegt, innerhalb von 1 Std. 20 Min. zurück ?
Lösung :
Bringen Sie die Teilung „60“ an der äußeren Skala mit der Markierung „▲“ von SPEED INDEX an der inneren Skala zur Deckung.
Ergebnis: Der Teilung „1:20“ an der inneren Skala entspricht 80 km als Entfernung.
[Berechnung der Kraftstoffverbrauchsrate (pro Stunde)]
![[Berechnung der Kraftstoffverbrauchsrate (pro Stunde)]](/cms/global/support/exterior/images/ext_motor_fuelratio.png)
Aufgabe :
Wie hoch ist die Kraftstoffverbrauchsrate (in Liter/h) , wenn 30 Liter Kraftstoff in 5 Std. Fahrzeit verbraucht werden ?
Lösung :
Bringen Sie die Teilung „30“ an der äußeren Skala mit der Teilung „5:00“ an der inneren Skala zur Deckung.
Ergebnis: Der Markierung „▲“ von SPEED INDEX an der äußeren Skala entspricht die Teilung „60“ an der äußeren Skala; also beträgt die Rate 6 Liter/h.
[Berechnung des Kraftstoffverbrauchs]
![[Berechnung des Kraftstoffverbrauchs]](/cms/global/support/exterior/images/ext_motor_fuel.png)
Aufgabe :
Wie viel Kraftstoff wird bei einer Fahrzeit von 5 Stunden verbraucht, wenn die Kraftstoffverbrauchsrate des Fahrzeugs 7 Liter/h beträgt ?
Lösung :
Bringen Sie die Teilung „70“ an der äußeren Skala mit der Markierung „▲“ von SPEED INDEX an der inneren Skala zur Deckung.
Ergebnis: Die Teilung „35“ an der äußeren Skala entspricht der Teilung „5:00“ an der inneren Skala, also beträgt der Kraftstoffverbrauch 35 Liter.
[Berechnung der Fahrzeit]
![[Berechnung der Fahrzeit]](/cms/global/support/exterior/images/ext_motor_time.png)
Aufgabe :
Wie viele Stunden lang kann ein Fahrzeug mit einer Kraftstoffverbrauchsrate von 8 Liter/h mit 40 Liter Kraftstoff fahren ?
Lösung :
Bringen Sie die Teilung „80“ an der äußeren Skala mit der Markierung „▲“ von SPEED INDEX an der inneren Skala zur Deckung.
Ergebnis: 5 Stunden – 5:00 auf der inneren Skala entspricht 40 auf der äußeren Skala.
Verwenden der Flugsport-Funktion
[Berechnung der zum Zurücklegen einer bestimmten Flugstrecke erforderlichen Flugzeit]
![[Berechnung der zum Zurücklegen einer bestimmten Flugstrecke erforderlichen Flugzeit]](/cms/global/support/exterior/images/ext_avi_time.png)
Aufgabe :
Wie lange braucht ein Flugzeug, das sich mit einer. Durchschnittsgeschwindigkeit von 180 Knoten bewegt, um 450 Seemeilen zurückzulegen ?
Lösung :
Bringen Sie die Teilung „18“ an der äußeren Skala mit der Markierung „▲“ von SPEED INDEX an der inneren Skala zur Deckung.
Ergebnis: Die Teilung „45“ an der äußeren Skala entspricht der Teilung „2:30“ an der inneren Skala, also benötigt das Flugzeit 2 Std. 30 Min., um diese Strecke zurückzulegen.
[Berechnung der Flugstrecke]
![[Berechnung der Flugstrecke]](/cms/global/support/exterior/images/ext_avi_distance.png)
Aufgabe :
Wie viele Seemeilen legt ein Flugzeug, das sich mit einer Durchschnittsgeschwindigkeit von 210 Knoten bewegt, innerhalb einer Flugzeit von 40 Minuten zurück ?
Lösung :
Bringen Sie die Teilung „21“ an der äußeren Skala mit der Markierung „▲“ von SPEED INDEX an der inneren Skala zur Deckung.
Ergebnis: Die Teilung „14“ an der äußeren Skala entspricht der Teilung„40“ an der inneren Skala, also legt das Flugzeug 140 Seemeilen zurück.
[Berechnung der Kraftstoffverbrauchsrate (pro Stunde)]
![[Berechnung der Kraftstoffverbrauchsrate (pro Stunde)]](/cms/global/support/exterior/images/ext_avi_consumptionrate.png)
Aufgabe :
Wie hoch ist die Kraftstoffverbrauchsrate (in Liter/h) , wenn 120 Gallonen Kraftstoff in 30 Min. Flugzeit verbraucht werden ?
Lösung :
Bringen Sie die Teilung „12“ an der äußeren Skala mit der Teilung „30“ an der inneren Skala zur Deckung.
Ergebnis: Der Markierung „▲“ von SPEED INDEX an der inneren Skala entspricht die Teilung „24“ an der äußeren Skala, also beträgt die Rate 240 Gallonen/h.
[Berechnung des Kraftstoffverbrauchs]
![[Berechnung des Kraftstoffverbrauchs]](/cms/global/support/exterior/images/ext_avi_fuelconsumption.png)
Aufgabe :
Wie viele Gallonen Kraftstoff werden bei einer Kraftstoffverbrauchsrate von 250 Gallonen/h für eine Flugzeit von 6 Stunden benötigt ?
Lösung :
Bringen Sie die Teilung „25“ an der äußeren Skala mit der Markierung „▲“ von SPEED INDEX an der inneren Skala zur Deckung.
Ergebnis: Der Teilung „15“ an der äußeren Skala entspricht die Teilung„6:00“ an der äußeren Skala, also werden 1.500 Gallonen benötigt.
[Berechnung der Flugzeit]
![[Berechnung der Flugzeit]](/cms/global/support/exterior/images/ext_avi_timefuel.png)
Aufgabe :
Wie viele Stunden lang kann ein Flugzeug bei einer Kraftstoffverbrauchsrate von 220 Gallonen/h mit 550 Gallonen Kraftstoff fliegen ?
Lösung :
Bringen Sie die Teilung „22“ an der äußeren Skala mit der Markierung „▲“ von SPEED INDEX an der inneren Skala zur Deckung.
Ergebnis: Der Teilung „55“ an der äußeren Skala entspricht die Teilung „2:30“ an der äußeren Skala, also kann das Flugzeug 2 Std. 30 Min. lang fliegen.
